Математика

		Зеркальная симметрия (осевая)
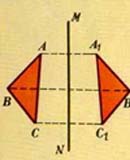
	На рисунке показан простой пример объекта и его зазеркального двойника – треугольник ABC и треугольник А1В1С1 (здесь MN – пересечение плоскости зеркала с плоскостью рисунка). Каждой точке объекта соответствует определённая точка зазеркального двойника. Эти точки находятся на одном перпендикуляре к прямой MN, по разные стороны и на одинаковом расстоянии от неё. Объект на рисунке выбран для простоты двухмерным. В общем случае объект (и соответственно его зазеркальный двойник) является трёхмерным.
Все знают, что увидеть зазеркальный двойник объекта совсем нетрудно. Достаточно поместить освещённый объект перед плоским зеркалом и заглянуть в это зеркало. Обычно считают, что наблюдаемый в зеркале двойник является точной копией самого объекта. В действительности же это не совсем так. Зеркало не просто копирует объект, а меняет местами (переставляет) передние и задние по отношению к зеркалу части объекта. В сравнении с самим объектом его зазеркальный двойник оказывается «вывернутым» вдоль направления, перпендикулярного к плоскости зеркала. Зазеркальный двойник не является точной копией объекта. Ведь объект и его двойник различаются только своей ориентации: они развёрнуты навстречу друг другу.
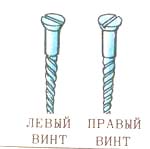
Чтобы получить зазеркальный двойник, не прибегая к отражению в зеркале, надо изменить вращение конуса на противоположное. Впрочем, можно обойтись и без вращения конуса. Достаточно из конуса винт. Винт-объект и винт-двойник имеют разные направления нарезки: чтобы ввинтить в дерево винт-объект, надо вращать его головку по часовой стрелке, а чтобы ввинтить винт-двойник, - против часовой стрелки. Первый винт называют правым винтом, а второй – левым. Мы привыкли пользоваться правыми винтами. Зазеркальные двойники правых винтов, то есть левые винты, у нас практически не применяются.
Итак, мы убедились, что объект и его зазеркальный двойник при всей своей схожести могут быть разными, не совместимыми друг с другом объекты. В одних случаях это различие не слишком бросается в глаза; например, можно не обратить внимание на то, что у вас родинка находится на правой щеке, а у вашего зазеркального двойника на левой. В других случаях различие становится настолько вопиющим, что приходится только удивляться, как на него не обращали внимание раньше. Достаточно сравнить какой-нибудь текст с его зазеркальным двойником. Попробуйте читать книгу, глядя не в неё, а в её отражение в зеркале. Или, что ещё хуже, попробуйте написать хотя бы строчку, глядя не на лист бумаги, а на его зеркальное изображение. Предположим, что одна половина объекта является зеркальным двойником по отношению к другой его половине, то такой объект называют зеркально симметричным. Он преобразуется сам в себя при отражении в соответствующей зеркальной плоскости; эту плоскостью называют плоскостью симметрии. В случае двухмерного (плоского) объекта вместо плоскости симметрии рассматривается ось симметрии – линия пересечения плоскости симметрии с плоскостью объекта. В случае одномерного (линейного) объекта рассматривается центр симметрии – точка пересечения прямой объекта с плоскостью симметрии.
	Одномерный объект имеет не более одного центра симметрии. Двухмерный объект может иметь несколько осей симметрии, а трёхмерный – несколько плоскостей симметрии. Так, правильный шестиугольник имеет шесть осей симметрии (красные прямые на рисунке).
*Энантиоморфы* – это пара зеркально асимметричных объектов (фигур), являющихся зеркальным изображением один другого. Иными словами, энантиоморфы – это объект и его зазеркальный двойник при условии, что сам объект зеркально асимметричен. Энантиоморфами могут быть отдельные объекты, но могут быть и половинки соответствующим образом разрезанного объекта. Чтобы различить энантиоморфы в данной паре, вводят обозначения «левый» и «правый». Один из энантиоморфов левый, а другой правый. Не имеет принципиального значения, какой именно назван левым (правым); это вопрос договоренности, традиции, привычки.
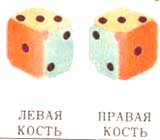
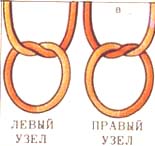
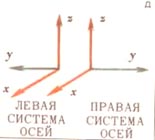
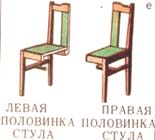
На рисунках приведены примеры трехмерных энантиоморфов: а) левый и правый винты; б) левая и правая игральные кости; в) левый и правый узлы; г) левая и правая перчатки; д) левая и правая системы координатных осей; е) левая и правая половинки стула, разрезанного по плоскости симметрии.