Математика

		Поворотная симметрия
Предположим, что объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360°/n (или кратный этой величине), где n = 2, 3, 4, … В этом случае о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка. Рассмотрим примеры со всеми известными буквами «И» и «Ф». Что касается буквы «И», то у нее есть так называемая поворотная симметрия. Если повернуть букву «И» на 180° вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой. Иными словами, буква «И» симметрична относительно поворота на 180°. Заметим, что поворотной симметрией обладает также буква «Ф».
Еще одним примером поворотной симметрии является египетская пирамида, которая тоже обладает поворотной симметрией. Она совмещается сама с собой, если мысленно повернуть ее на угол 90° вокруг вертикальной оси, проходящей через вершину пирамиды. В приводившихся ранее примерах с буквами «И» и «Ф» мы встречались с поворотной осью 2-ого порядка, а в примере с египетской пирамидой – с поворотной осью 4-го порядка.
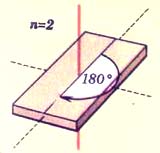
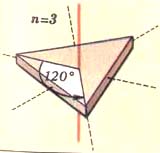
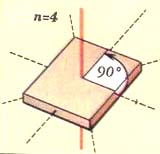
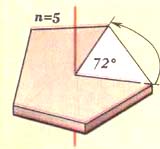
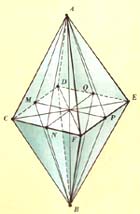
На рисунке даны примеры простых объектов с поворотными осями разного порядка – от 2-го до 5-го.

У трехмерного объекта может быть несколько поворотных осей. Например, первый объект на рисунке имеет не одну, а три поворотные оси 2-го порядка, второй объект имеет наряду с поворотной осью 3-го порядка три поворотные оси 2-го порядка, третий объект имеет наряду с поворотной осью 4-го порядка четыре поворотные оси 2-го порядка (дополнительные поворотные оси показаны на рисунке штриховыми прямыми).
Интересна поворотная симметрия кругового цилиндра. Он имеет бесконечное число поворотных осей 2-го порядка и одну поворотную ось бесконечно высокого порядка.
	Для описания симметрии конкретного объекта надо указать все поворотные оси и их порядок, а также все плоскости симметрии. Рассмотрим, например, геометрическое тело, составленное из двух одинаковых правильных четырехугольных пирамид. Оно имеет одну поворотную ось 4-го порядка (ось АВ), четыре поворотные оси 2-го порядка (оси СЕ, DF, MP, NQ), пять плоскостей симметрии (плоскости CDEF, AFBD, ACBE, AMBP, ANBQ).