|
|
Зеркально-поворотная симметрия |
|
|
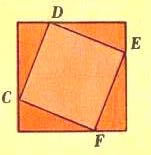
Доказать, что существует такой вид симметрии, мы предлагаем вам самим. Вырежьте из плотной бумаги квадрат и впишите внутрь его косо другой квадрат (рис.1). | |
|
Затем
отогните углы бумаги по линиям,
ограничивающим внутренний квадрат
(соседние углы отгибаются в
противоположные стороны). В результате
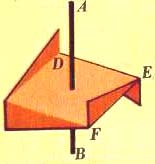
получите объект, показанный на рисунке (рис.2).
Он
имеет поворотную ось 2-го порядка (ось АВ)
и не имеет плоскостей симметрии. Будем
рассматривать изделия сначала сверху, а
затем снизу (с противоположной стороны
листа бумаги). Мы обнаружим, что никакого
различия между «верхом» и «низом» нет; в
обоих случаях объект выглядит одинаково.
В связи с этим возникает мысль, что
поворотная симметрия 2-го порядка не
исчерпывает всей симметрии данного
объекта. |
|
|
|
||
|
||
| Дополнительная симметрия, которой обладает наш объект, - это так называемая зеркально-поворотная симметрия: объект совмещается сам с собой в результате поворота на 90° вокруг оси АВ и последующего отражения в плоскости CDEF. Ось АВ называют зеркально-поворотной осью 4-го порядка. Таким образом, здесь наблюдается симметрия относительно двух последовательно выполняемых операций – поворота на 90 и отражения в плоскости, перпендикулярной к оси поворота. | ||