УДИВЛЯЮЩИЙ УЗОР

Трудно найти человека, не любовавшегося орнаментами – этими удивительными рисунками, часто встречающимися в декоративном художественном творчестве. В них можно обнаружить затейливое сочетание переносной, зеркальной и поворотной симметрий. За примером орнамента не надо далеко ходить – взгляните на рисунок обоев, которыми оклеены стены вашей комнаты. Некоторые образцы орнаментов показаны на рисунках.

Среди них два созданы известным современным голландским художником Эшером – орнаменты «Летящие птицы» и «Ящерицы».

 В основе любого орнамента лежит одна из пяти плоских решеток.

С переносной симметрией связано понятие двухмерной периодической структуры – плоской решетки. Плоская решетка может быть образована в результате пересечения двух семейств параллельных, равноотстоящих друг от друга прямых.

Точки пересечения прямых называют узлами решетки. Чтобы задать решетку достаточно задать ее элементарную ячейку и затем переносить эту ячейку параллельно самой себе вдоль прямой АВ на расстояния, кратные а, либо вдоль прямой АС на расстояния, кратные b. Заметим, что элементарную ячейку данной решетки можно выбрать разными способами. Так, можно выбрать в качестве элементарной ячейку, которая на рисунке закрашена красным цветом. Однако можно было бы воспользоваться и любой из заштрихованных на рисунке ячеек. Переносная симметрия плоской решетки полностью определяется совокупностью двух векторов (векторы a и b на рисунке).

 Различают пять типов плоских решеток  (пять типов переносной симметрии на плоскости):   

a). a=b, g=90° (квадратная решетка)

б) a¹b,g¹90° (прямоугольная решетка)

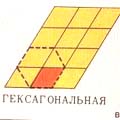
 в). a=b, g=60° (гексагональная решетка)

г). a=b, g¹90°, g¹60° (ромбическая решетка)

д). a¹b, g¹90° (косая решетка)

С переносной симметрией в трехмерном пространстве связано понятие трехмерной периодической структуры – пространственной решетки. Такая решетка может рассматриваться как результат пересечения трех семейств трех параллельных плоскостей. Переносная симметрия трехмерной решетки определяется совокупностью трех векторов, задающих элементарную ячейку решетки. На рисунке показана ячейка решетки, задаваемая векторами a, b, c. В простейшем случае длины всех ребер ячейки равны между собой, а углы между ребрами составляют 90°. В этом случае говорят о кубической решетке. Всего же существует 14 типов пространственных решеток, различающихся по типу переносной симметрии. Иначе говоря, существуют 14 типов решеток Бравэ (Бравэ – французский кристаллограф 19 века).

В простейшем случае орнамент характеризуется только переносной симметрией. Таков, например, орнамент «Летящие птицы». Чтобы построить этот орнамент, надо выбрать соответствующую косую решетку «заполнить» элементарную ячейку решетки определенным рисунком и затем многократно повторить этот рисунок за счет переносов ячейки без изменения ее ориентации. На рисунке элементарная ячейка орнамента заштрихована. Заметим, что площадь ячейки равна сумме площадей, занимаемых изображениями птиц разного цвета.